The curious case of Bloom Filters
A quick introduction to Bloom Filter, a probablistic data structure.
A Bloom Filter is a probabilistic data structure used to check the presence of an element in a large dataset.
Unlike traditional collections like a HashSet, a Bloom Filter is NOT used to store the data itself but is only used to check its absence with surety (or its presence with an accepted tolerance level). This makes it space efficient as the presence or absence can be denoted by a single bit, whereas the records in the data set can be of any size.
A simple Bloom Filter can be created using the following:
- An upper bound on the number of entries we want to add. Let’s refer to this as
n. - A
BitSet or a boolean array of size
nwhere all the bits are initially set to0. - A set of hash functions that can map the data entries to individual index locations.

Empty Bloom Filter
Addition of records
Every record in the input dataset is passed through a set of hash functions that calculate a unique index for the entry within the limits of the bloom filter size \([0,n)\).
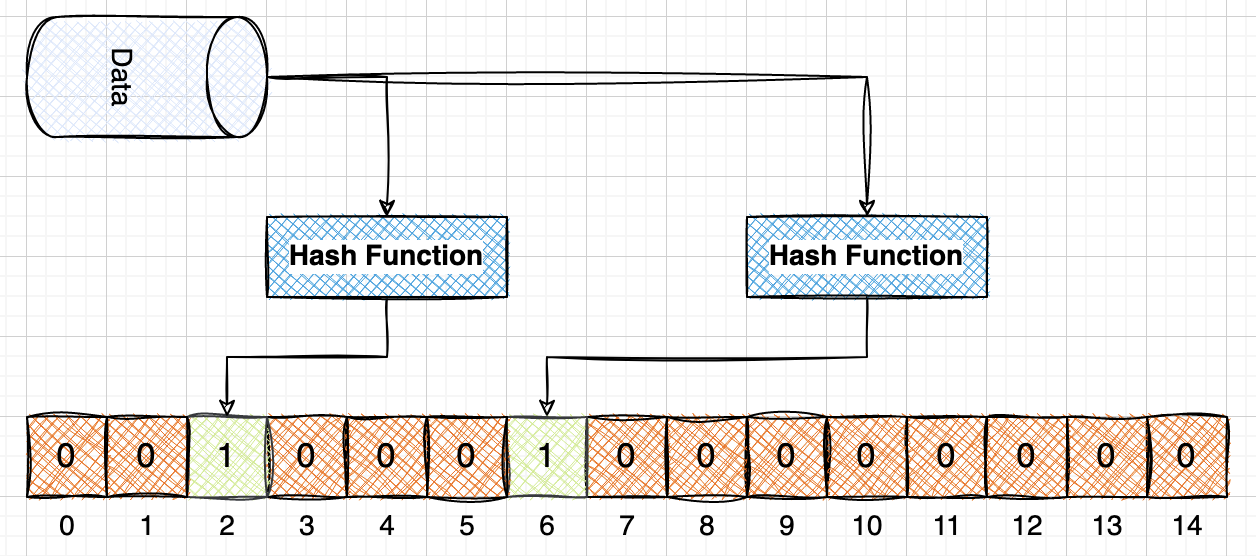
Bloom Filter Addition
As a result of the hash function mapping, the index locations are marked set(1), denoting the presence of the current record entry. Once all the entries are processed through the hash functions, the resultant bloom filter will have the corresponding indices set(1) and ready for reference.
Checking the presence of records
To check whether a specific entry is present, we must run it through the hash functions again and validate the corresponding indices.
- If either of the indices is NOT set, the record was not present in the original dataset.
- If both indices are set, the record may be present in the original dataset.
False Positive: Depending on the hash function(s) used and the upper limit n, we could experience false positives, which means that even if all the resultant indices are set, the record may still be missing.
For example, suppose we add more than n elements, or the hash function results in collisions due to the underlying implementation. In that case, we may find an index set (due to some other element with the same index resulting from hash functions) in the data structure, even when the entry was not present.
Implementations
Google Guava provides a thread-safe and lock-free implementation of BloomFilters that is very easy to use.
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
public class BloomFiltersExample{
public BloomFilter<Integer> create(int size, double acceptableFalsePositivityRate){
return BloomFilter.create(Funnels.integerFunnel(), size, acceptableFalsePositivityRate);
}
public boolean add(int input, BloomFilter<Integer> bloomFilter){
return bloomFilter.put(input);
}
public boolean checkPresence(int input, BloomFilter<Integer> bloomFilter){
return bloomFilter.mightContain(input);
}
}
As mentioned above, let’s write a couple of testcases to validate the behaviour:
def "test presence of elements when added element count less than the upper limit"() {
given: "an upper bound n for the total number of elements"
def n = 10
and: "an acceptable false positivity rate"
double fpr = 0.01
var bfExample = new BloomFiltersExample()
when: "the BF instance is created and elements are added"
def instance = bfExample.create(n, fpr)
IntStream.range(0, 7).forEach(val -> bfExample.add(val, instance))
then: "a valid instance is created"
instance != null
and: "instance is NOT empty"
instance.approximateElementCount() == 7
and: "no false positives are returned"
bfExample.checkPresence(entry, instance) == isPresent
where:
entry | isPresent
0 | true
1 | true
2 | true
11 | false
12 | false
}
The above mentioned test-case can be updated to demonstrate the false positive scenario by adding a lot more elements as compared to the upper limit:
def "test presence of elements when added element count more than the upper limit"() {
given: "an upper bound n for the total number of elements"
def n = 10
and: "an acceptable false positivity rate"
double fpr = 0.01
var bfExample = new BloomFiltersExample()
when: "the BF instance is created and elements are added"
def instance = bfExample.create(n, fpr)
IntStream.range(0, 50).forEach (val -> bfExample.add(val, instance))
then: "a valid instance is created"
instance != null
and: "instance is NOT empty"
instance.approximateElementCount() != 0
and: "no false positives are returned"
bfExample.checkPresence(entry, instance) == isPresent
where:
entry | isPresent
0 | true
1 | true
2 | true
11 | true
12 | true
}
From this, we can conclude that:
- A false result will guarantee that the value is NOT present in the original input. Hence a false negative is never the case.
- A true indicates that the value may be present - false positive is possible.
- The probability of a false positive is inversely proportional to the number and quality of hash functions. It also depends on the size of the underlying data structure and the number of elements in it.
Bloom filters do not support removing an element, as clearing the corresponding bits may also clear bits of some other entries.
Bloom filters are of great use when dealing with large datasets to avoid extra IO operations like in case of distributed databases or remote file systems. In those scenarios, the IO operation is only performed if confirmed by the filter, which reduces the overall resource-intensive operation’s count.
You can check the complete example in the Github repository.
That is all for this post. If you want to share any feedback, please drop me an email, or contact me on any social platforms. I’ll try to respond at the earliest. Also, please consider subscribing for regular updates.